I've previously taken a class, Introduction to Probability (Stat 240), which introduced me to basic set theory. The class was initially difficult for me, as it seemed to me that set theory was a completely different way of thinking about grouping. With that said, I ended up doing well and coming to understand set theory well. Thus this simple introduction does not present anything too new.
Yet, there are some things that were unclear in the reading for me, and difficult to understand. Namely, the new assignment of symbols for different sets:
| symbol | for the set of |
| N | natural numbers (positive integers) |
| Z | integers |
| Q | rational numbers |
| I | irrational numbers |
| R | real numbers |
| C | complex numbers |
The different groupings of numbers were difficult for me to understand at first, but I ended up understanding it by looking at examples.
Also difficult for me was the concept of differences. I didn't understand how you could take one set and subtract another set from it. But after seeing the Venn Diagram for it (which I pasted below), it was a lot more clear.
What was the most interesting part of the material?
Reading through this introduction to set theory and thinking back on past courses I have had on set theory made me think about the interesting way that set theory teaches you to think about grouping. I've had some experience in segmentation with work that I've done. With these segments, set theory was very helpful in doing more work and making sense of the different groups. How? By taking different segments, and sets of segments, and subsets, and complements of these segments.
I think that while the learning of set theory can sometimes seem rote (for me it is difficult to read through examples that do not originally seem to have immediate application to real world problems), the way that simple set theory can be used and applied is powerful. The different symbols encapsulate important methods of splitting up data and expand your way of thinking about grouping.
Below is an example of different symbols, that even to the student, can be used powerfully for grouping. These symbols allow you to think and express grouping in ways that are invaluable to solving problems.

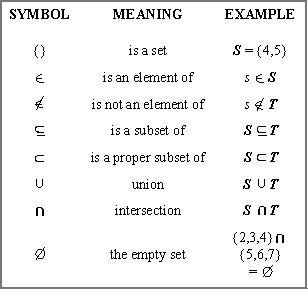
No comments:
Post a Comment